Compressible Gas Flow in Pipelines - FluidFlow
Many equations used for the solution of gas flow in pipelines do not take into consideration rigorously the deviation of natural gas from ideal gas behaviour. For low-pressure gas flow, the error is considered low, however, for high pressures, high flow rates, low temperatures or the closer the gas is to change in phase state, this error can be significant. This deviation from ideality must be taken into consideration. It is therefore important when modeling gas pipe flow systems to use a
software tool which doesn’t make the simplifying assumptions of gas ideality.
FluidFlow does not make these simplifying assumptions but solves for real gas conditions using an equation of state. The simplified application of the ideal gas law (Pv = nRT) makes several assumptions as outlined below;
– Particles in an ideal gas are in constant, random, straight-line motion.
– The volume occupied by the particles is negligible relative to the volume of the enclosure.
– The collisions between particles are elastic with no loss of kinetic energy.
– There are no intermolecular forces acting between the particles in an ideal gas.
An ideal gas assumes a large number of point particles colliding elastically. It neglects any short-range intermolecular forces resulting from repulsion or attraction due to molecular charges and the fact that molecules have a finite volume, i.e. are not infinitely small! This means a real gas is not infinitely compressible whereas an ideal gas has no such limitations.
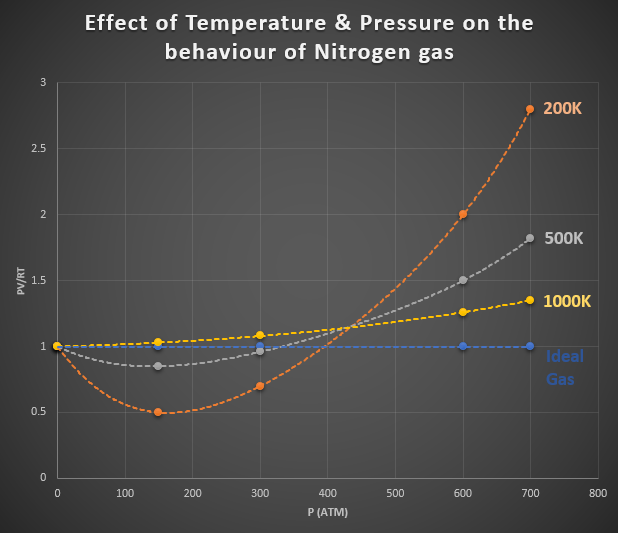
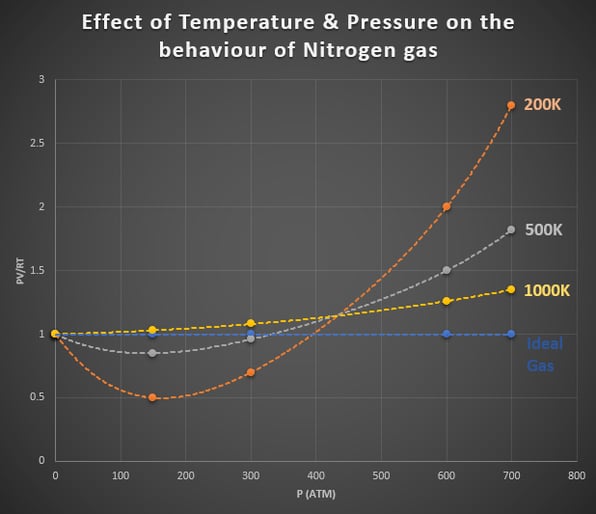
Although the ideal gas law may be a useful simplified description of gases, all real gases fail to obey this relationship to some degree. The extent to which a real gas departs from ideal behaviour can be seen by rearranging the ideal-gas equation to solve for n (PV/RT = n). This form of the equation tells us that for 1 mol of an ideal gas (n=1), the quantity PV/RT equals 1 at all pressures. However, under the conditions of real gas flow outlined earlier, a product of PV divided by RT is no longer equal to one.
In the graph shown in Figure 1, we can see the deviation of nitrogen gas from ideal gas behaviour. On the y-axis, we have the product of PV/RT. On the x-axis, were have pressure. The dashed blue line shows the behaviour of an ideal gas for which the product of PV/RT is equal to one under any conditions. The orange, grey and yellow dashed lines show the deviation of nitrogen gas from ideal gas behaviour at different temperatures and pressures. These dashed lines show a considerable deviation of ideal gas behaviour. Notice how the conditions that produce this curve are high pressure and low temperature.
Figure 1: Effect of Temperature & Pressure on the Behaviour of Nitrogen Gas.
As high pressures, the deviation from ideal behaviour is considerable and is different for each gas. Real gases, therefore, do not behave ideally at high pressures.
It is noted in many literature sources that the ideal gas equations can be used with some degree of accuracy under certain specific conditions, i.e. at low pressures. Caution should, however, be exercised when applying gas ideality and a thorough check of system operating conditions to ensure the design solution falls within the criteria.
FluidFlow doesn’t make the simplifying and often error-prone assumption of applying gas ideality but solves for real gas conditions using an equation of state. The software, therefore, takes into account the gas compressibility factor (Z) and solves gas flow systems using a marching algorithm for incremental pipe length. This ensures a much higher level of solution accuracy.
The solution of gas flow systems becomes more complex when dealing with gas mixtures and large systems. It is recommended that a suitable software tool should is selected to design and solve gas flow systems in an attempt to eliminate the potential for errors resulting from the simplification of ideal gas flow.
In conclusion, let’s ponder the following quote:
“Perfect gases are like perfect people: They do not exist.”