To obtain maximum accuracy in gas calculations, particularly in systems where large pressure losses occur, the Joule-Thomson effect needs to be included in the solution. The J-T effect describes the increase or decrease in temperature of a real gas (as opposed to an ideal gas) or liquid as it flows from an area of high pressure to an area of low pressure without heat transfer to or from the fluid and no external mechanical work extracted from the fluid. An example of such a scenario would be a gas flowing through a perfectly thermally insulated throttling device such as a valve, nozzle or orifice plate.
The temperature change experienced during a Joule-Thomson expansion is quantified by the Joule-Thomson coefficient.
Joule-Thomson Coefficient
The temperature change arising from a reduction in pressure at constant enthalpy in the Joule-Thomson process can be expressed as:
μJT = (∂T/∂P)H
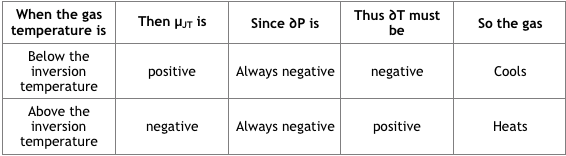
The value of μJT (oC/bar) depends on the gas type as well as its pressure and temperature before expansion. This coefficient may be either positive (cooling) or negative (heating). For all real gases, the value of μJT will equal zero at some point called the inversion point and the J-T inversion temperature is the temperature where the coefficient changes sign (where the coefficient equals zero).
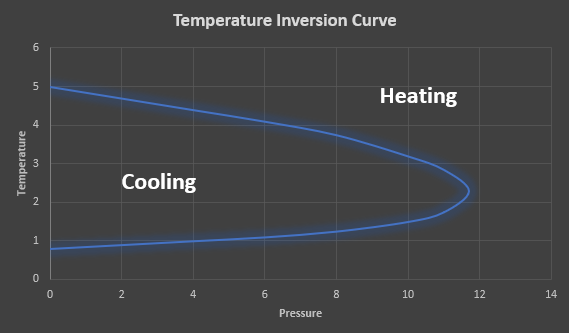
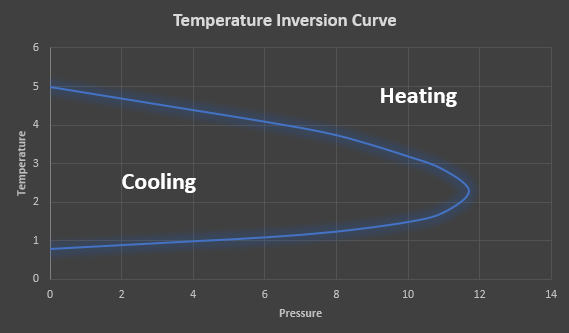
The inversion temperature represents the temperature of a gas at which a reduction in pressure causes no temperature change. Above this temperature, the gas heats on expansion and below this temperature, the gas cools on expansion. When a real gas expands through a throttling device, the gas temperature may either increase or decrease depending on the initial gas pressure and temperature. Figure 1 provides an illustration of a typical temperature inversion curve.
Figure 1: Temperature inversion Curve.
In gas expansion, the gas pressure reduces and thus the sign of ∂P is always negative. The following table explains when the Joule-Thomson effect heats or cools a real gas.
It is worth noting at this point that, there is no Joule-Thomson effect for an ideal gas. The value of μJT, therefore, equals zero, i.e., in theory, ideal gases neither heat or cool during expansion at constant enthalpy.
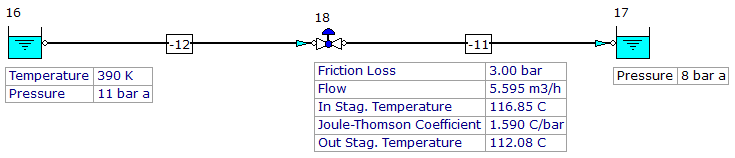
FluidFlow takes account of the Joule-Thomson coefficient when solving gas flow systems using real gas conditions. Figure 2 details the calculation of Joule-Thomson coefficient for a pressure control valve in a pipeline transporting a mixture of n-butane and n-pentane at a pressure of 11bar and temperature of 390K.
Figure 2: FluidFlow J-T Coefficient Calculation.
