Non-Newtonian Fluids
Non-Newtonian fluids are encountered in a wide and varied range of industrial processes including food, mining and minerals, pharmaceuticals, pulp and paper processing and other products in the form of pastes, slurries, concentrated solid suspensions or emulsions. Examples include coal slurries, mud, sludge, paint, ketchup, mayonnaise, blood, shaving cream, toothpaste, dilute solutions etc. These fluids regularly exhibit non-Newtonian viscous properties and it is important for the designer to be familiar with the flow behaviour of such fluids, how to characterise the fluid physical properties of these fluids and how to use these properties to predict flow behaviour in process piping systems.
Newtonian fluids exhibit a linear relationship between shear rate and shear stress. The slope μ (viscosity) is constant and therefore, the viscosity of a Newtonian fluids is independent of shear rate. Non-Newtonian fluids on the other hand typically exhibit either shear thinning or shear thickening behaviour and in some cases, exhibit a yield stress, i.e. a stress level which must be overcome before the fluid begins to flow. There are a number of common rheology models or methods often used to characterise Non-Newtonian fluids. These include the Herschel-Bulkley, Power Law, Casson and Bingham Plastic models, all of which are available in FluidFlow software.
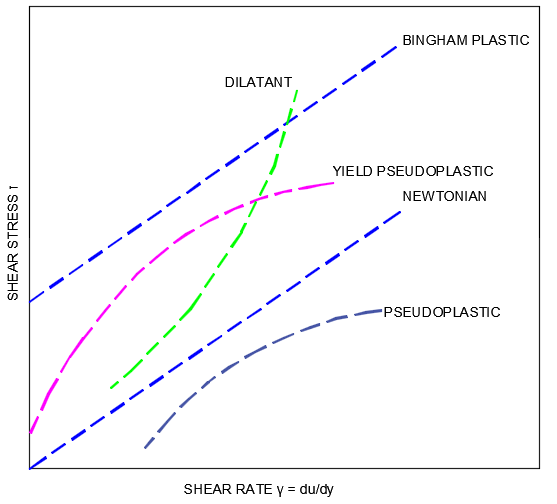
The viscosity of a Non-Newtonian fluid can take various forms, some of which are outlined in Figure 1. The flow behaviour classes outline in Figure 1 are Bingham Plastic, Dilatant, Pseudoplastic and Yield Pseudoplastic.
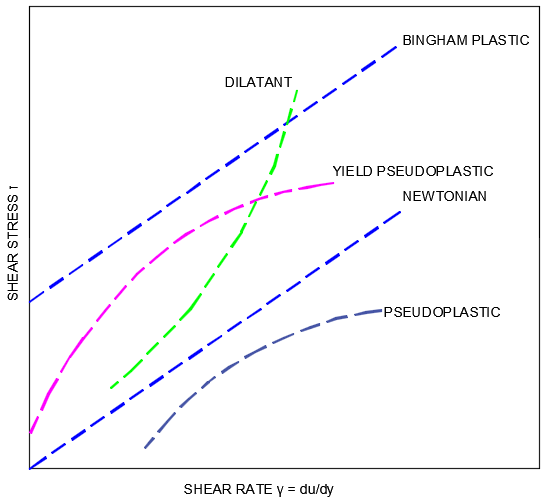
Figure 1: Non-Newtonian Fluids (Shear Stress vs Shear Rate).
A Bingham plastic fluid exhibits
Dilatant fluids exhibit shear thickening properties, i.e. the fluid viscosity increases with the rate of applied shear stress. A mixture of cornstarch and water is a good reference example of a dilatant fluid.
Pseudoplastic fluids such as paint and ketchup exhibit shear thinning properties where the viscosity decreases with the rate of applied shear stress.
Yield Pseudoplastic fluids are similar to Pseudoplastic fluids with the exception that they exhibit a yield stress level, i.e. the fluid behaves as a Pseudoplastic fluid above the yield stress level.
Figure 2 provides an illustration of typical shear rate vs shear stress data for a non-Newtonian fluid. We can see from the linear graph plot on the left that curve relationship for fluid is y = 0.0197x + 52.68 where the line has a slope of 0.0197 (coefficient of rigidity) and an intercept of 52.67 Pa (Yield Stress). This fluid data has been defined as a Bingham Plastic fluid in the FluidFlow database as shown on the right of Figure 2. We can see the data-points together with the curve equation is shown in FluidFlow providing a relationship of shear stress = 0.0197(shear rate) + 52.68.
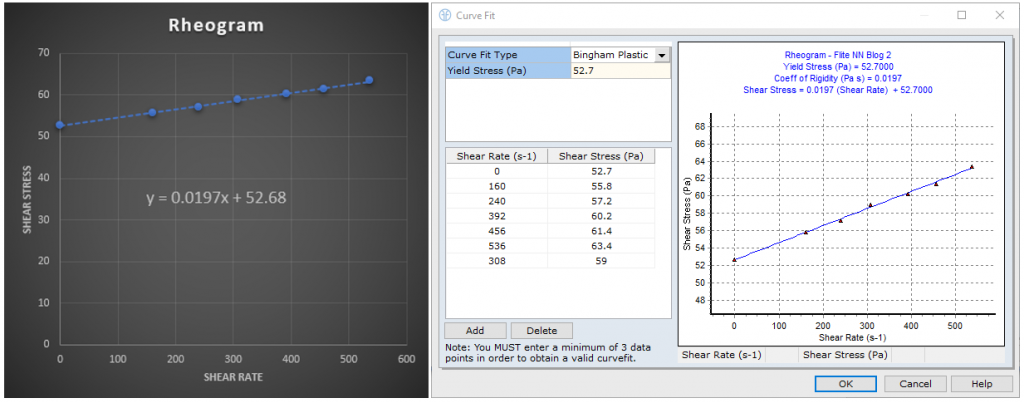
Figure 2: Non-Newtonian Fluids (Shear Stress vs Shear Rate).
FluidFlow helps you characterise non-Newtonian fluids as you can define your data-points of shear rate vs shear stress and swap through the four available rheology relationships (Herschel-Bulkley, Power Law, Casson and Bingham Plastic) and choose the relationship/curve-fit which best represents the defined data-points. A simple yet very effective tool.
Figure 3 provides an illustration of a non-Newtonian pipe flow system from a mining application as modeled in FluidFlow. The system includes two pumps in parallel transporting a Bingham Plastic fluid through over 8,900 m of pipework with changing elevation.
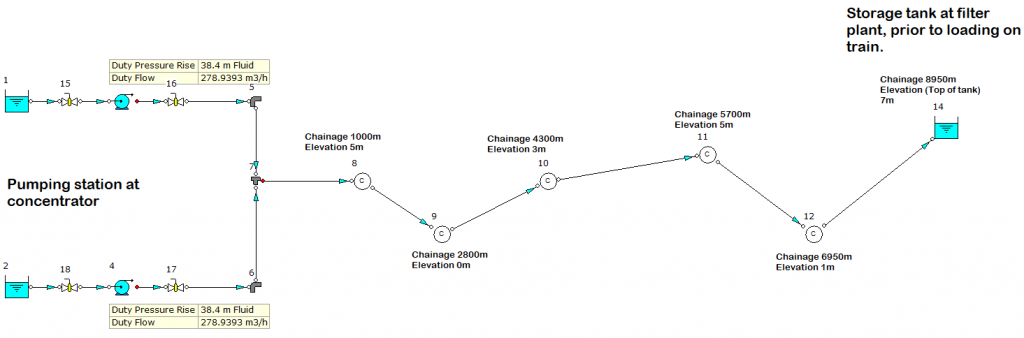
Figure 3: Overland Non-Newtonian Pipe Flow System.
Figure 4 provides an illustration of a red mud pipe flow system as modeled in FluidFlow. The system includes eight pumps transporting a non-Newtonian fluid through over 7,300 m of pipework.
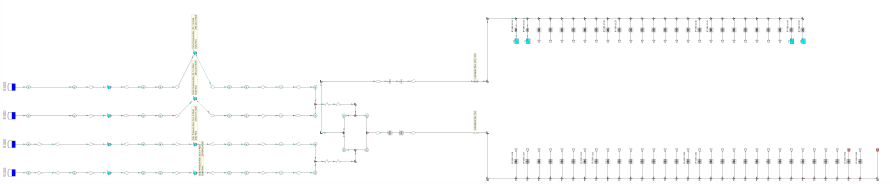
Figure 4: Red Mud Pipe Flow System.
Some typical applications where FluidFlow is used to model Non-Newtonian flow systems include:
- Mine Tailings Systems.
- Metal Concentrate Processing.
- Food Industry Applications.
- Dredging and Waste Systems.
- Medical Devices/Instrumentation (Blood Flow)
